Another explainer on a fun, esoteric topic: optimizing code with SIMD (single instruction multiple data, also sometimes called vectorization). Designing a good, fast, portable SIMD algorithm is not a simple matter and requires thinking a little bit like a circuit designer.

Here’s the mandatory performance benchmark graph to catch your eye.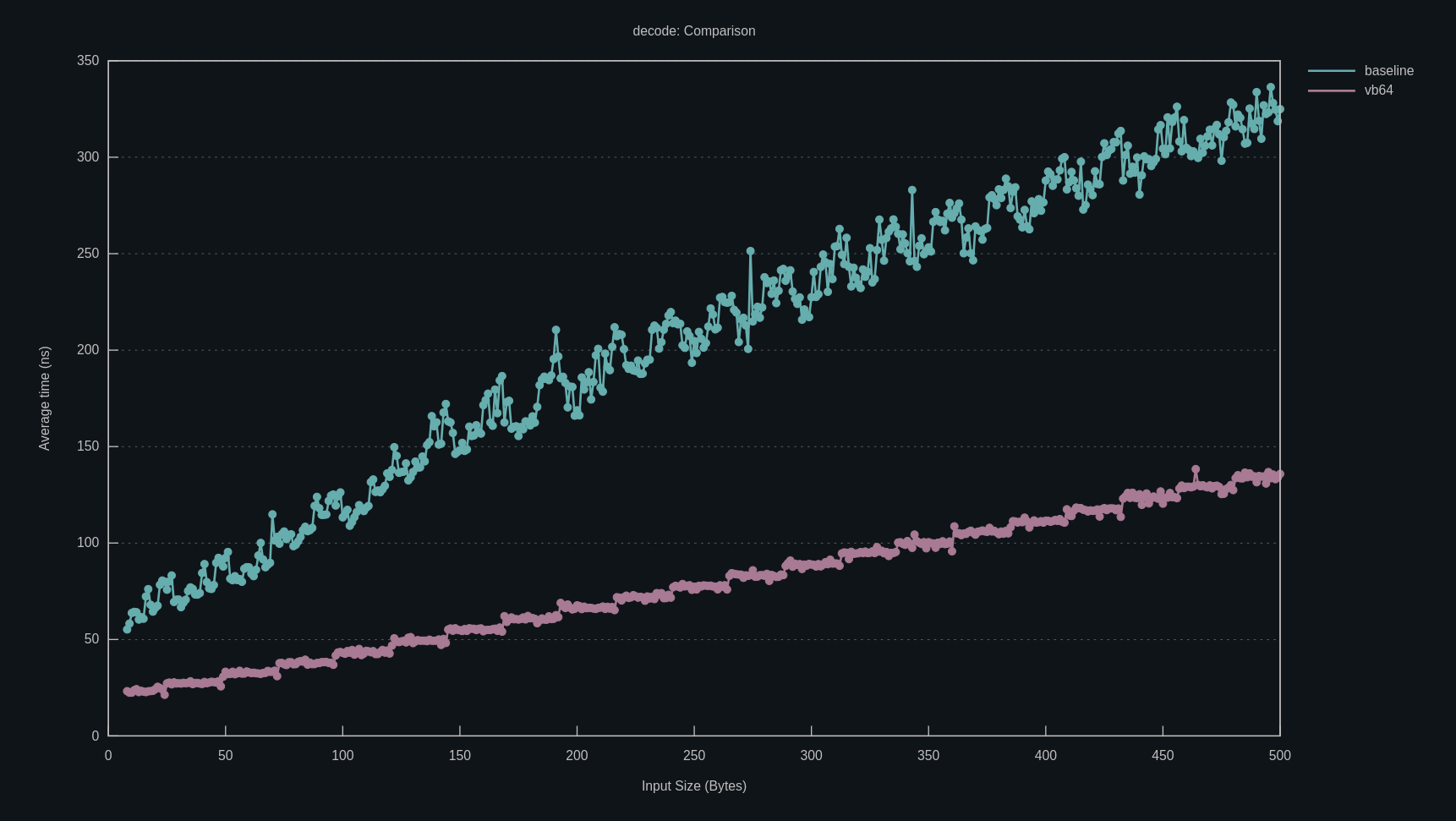

“SIMD” often gets thrown around as a buzzword by performance and HPC (high performance computing) nerds, but I don’t think it’s a topic that has very friendly introductions out there, for a lot of reasons.

• It’s not something you will really want to care about unless you think performance is cool.
• APIs for programming with SIMD in most programming languages are garbage (I’ll get into why).
• SIMD algorithms are hard to think about if you’re very procedural-programming-brained. A functional programming mindset can help a lot.

This post is mostly about vb64 (which stands for vector base64), a base64 codec I wrote to see for myself if Rust’s std::simd library is any good, but it’s also an excuse to talk about SIMD in general.

What is SIMD, anyways? Let’s dive in.

If you want to skip straight to the writeup on vb64, click here.

Problems with Physics

Unfortunately, computers exist in the real world^{[citation-needed]}, and are bound by the laws of nature. SIMD has relatively little to do with theoretical CS considerations, and everything to do with physics.

In the infancy of modern computing, you could simply improve performance of existing programs by buying new computers. This is often incorrectly attributed to Moore’s law (the number of transistors on IC designs doubles every two years). Moore’s law still appears to hold as of 2023, but some time in the last 15 years the Dennard scaling effect broke down. This means that denser transistors eventually means increased power dissipation density. In simpler terms, we don’t know how to continue to increase the clock frequency of computers without literally liquefying them.

So, since the early aughts, the hot new thing has been bigger core counts. Make your program more multi-threaded and it will run faster on bigger CPUs. This comes with synchronization overhead, since now the cores need to cooperate. All control flow, be it jumps, virtual calls, or synchronization will result in “stall”.

The main causes of stall are branches, instructions that indicate code can take one of two possible paths (like an if statement), and memory operations. Branches include all control flow: if statements, loops, function calls, function returns, even switch statements in C. Memory operations are loads and stores, especially ones that are cache-unfriendly.

Procedural Code Is Slow

Modern compute cores do not execute code line-by-line, because that would be very inefficient. Suppose I have this program:

let a = x + y;
let b = x ^ y;
println!("{a}, {b}");

There’s no reason for the CPU to wait to finish computing a before it begins computing b; it does not depend on a, and while the add is being executed, the xor circuits are idle. Computers say “program order be damned” and issue the add for a and the xor for b simultaneously. This is called instruction-level parallelism, and dependencies that get in the way of it are often called data hazards.

Of course, the Zen 2 in the machine I’m writing this with does not have one measly adder per core. It has dozens and dozens! The opportunities for parallelism are massive, as long as the compiler in your CPU’s execution pipeline can clear any data hazards in the way.

The better the core can do this, the more it can saturate all of the “functional units” for things like arithmetic, and the more numbers it can crunch per unit time, approaching maximum utilization of the hardware. Whenever the compiler can’t do this, the execution pipeline stalls and your code is slower.

Branches stall because they need to wait for the branch condition to be computed before fetching the next instruction (speculative execution is a somewhat iffy workaround for this). Memory operations stall because the data needs to physically arrive at the CPU, and the speed of light is finite in this universe.

Trying to reduce stall by improving opportunities for single-core parallelism is not a new idea. Consider the not-so-humble GPU, whose purpose in life is to render images. Images are vectors of pixels (i.e., color values), and rendering operations tend to be highly local. For example, a convolution kernel for a Gaussian blur will be two or even three orders of magnitude smaller than the final image, lending itself to locality.

Thus, GPUs are built for divide-and-conquer: they provide primitives for doing batched operations, and extremely limited control flow.

“SIMD” is synonymous with “batching”. It stands for “single instruction, multiple data”: a single instruction dispatches parallel operations on multiple lanes of data. GPUs are the original SIMD machines.

Lane-Wise

“SIMD” and “vector” are often used interchangeably. The fundamental unit a SIMD instruction (or “vector instruction”) operates on is a vector: a fixed-size array of numbers that you primarily operate on component-wise These components are called lanes.

SIMD vectors are usually quite small, since they need to fit into registers. For example, on my machine, the largest vectors are 256 bits wide. This is enough for 32 bytes (a u8x32), 4 double-precision floats (an f64x8), or all kinds of things in between.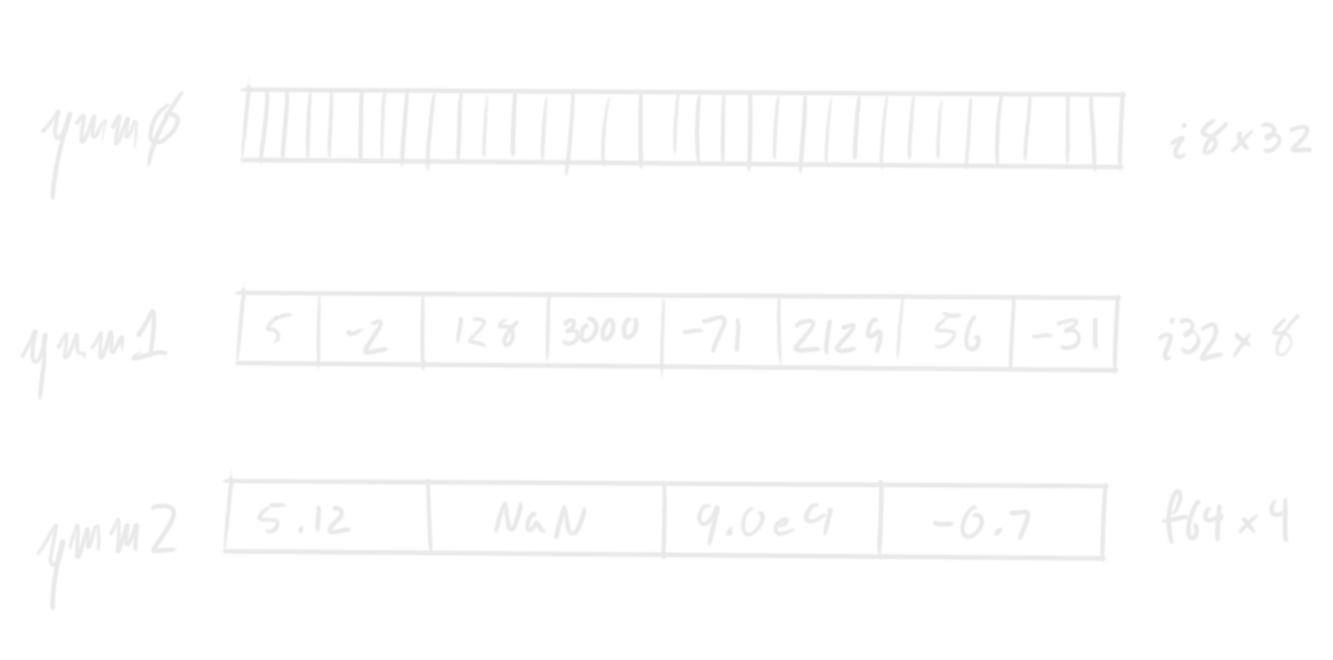

Although this doesn’t seem like much, remember that offloading the overhead of keeping the pipeline saturated by a factor of 4x can translate to that big of a speedup in latency.

One-Bit Lanes

The simplest vector operations are bitwise: and, or, xor. Ordinary integers can be thought of as vectors themselves, with respect to the bitwise operations. That’s literally what “bitwise” means: lanes-wise with lanes that are one bit wide. An i32 is, in this regard, an i1x32.

In fact, as a warmup, let’s look at the problem of counting the number of 1 bits in an integer. This operation is called “population count”, or popcnt. If we view an i32 as an i1x32, popcnt is just a fold or reduce operation:

pub fn popcnt(mut x: u32) -> u32 {
  let mut bits = [0; 32];
  for (i, bit) in bits.iter_mut().enumerate() {
    *bit = (x >> i) & 1;
  }
  bits.into_iter().fold(0, |total, bit| total + bit)
}

In other words, we interpret the integer as an array of bits and then add the bits together to a 32-bit accumulator. Note that the accumulator needs to be higher precision to avoid overflow: accumulating into an i1 (as with the Iterator::reduce() method) will only tell us whether the number of 1 bits is even or odd.

Of course, this produces… comically bad code, frankly. We can do much better if we notice that we can vectorize the addition: first we add all of the adjacent pairs of bits together, then the pairs of pairs, and so on. This means the number of adds is logarithmic in the number of bits in the integer.

Visually, what we do is we “unzip” each vector, shift one to line up the lanes, add them, and then repeat with lanes twice as big.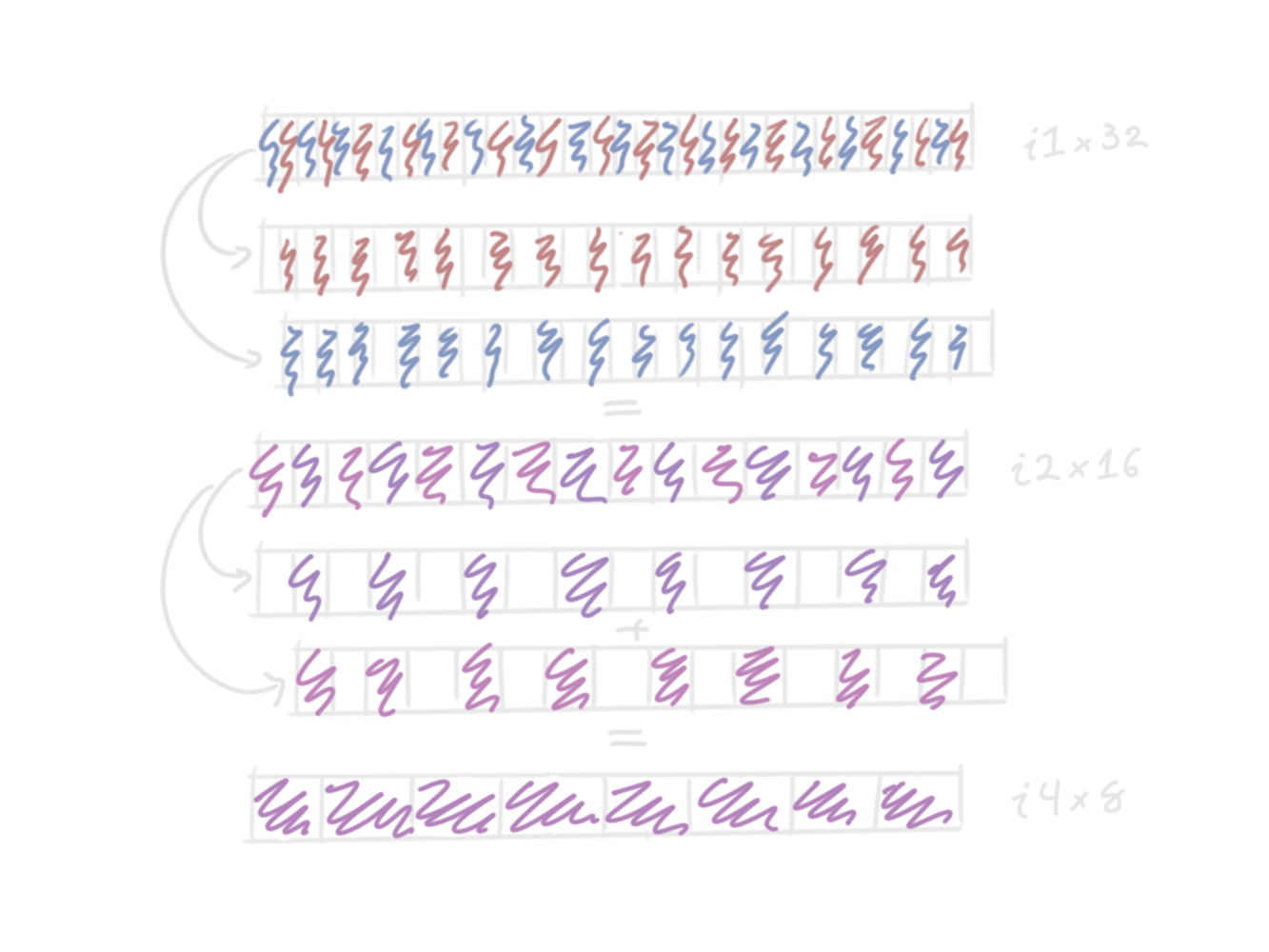

This is what that looks like in code.

pub fn popcnt(mut x: u32) -> u32 {
  // View x as a i1x32, and split it into two vectors
  // that contain the even and odd bits, respectively.
  let even = x & 0x55555555; // 0x5 == 0b0101.
  let odds = x & 0xaaaaaaaa; // 0xa == 0b1010.
  // Shift odds down to align the bits, and then add them together.
  // We interpret x now as a i2x16. When adding, each two-bit
  // lane cannot overflow, because the value in each lane is
  // either 0b00 or 0b01.
  x = even + (odds >> 1);

  // Repeat again but now splitting even and odd bit-pairs.
  let even = x & 0x33333333; // 0x3 == 0b0011.
  let odds = x & 0xcccccccc; // 0xc == 0b1100.
  // We need to shift by 2 to align, and now for this addition
  // we interpret x as a i4x8.
  x = even + (odds >> 2);

  // Again. The pattern should now be obvious.
  let even = x & 0x0f0f0f0f; // 0x0f == 0b00001111.
  let odds = x & 0xf0f0f0f0; // 0xf0 == 0b11110000.
  x = even + (odds >> 4); // i8x4

  let even = x & 0x00ff00ff;
  let odds = x & 0xff00ff00;
  x = even + (odds >> 8);  // i16x2

  let even = x & 0x0000ffff;
  let odds = x & 0xffff0000;
  // Because the value of `x` is at most 32, although we interpret this as a
  // i32x1 add, we could get away with just one e.g. i16 add.
  x = even + (odds >> 16);

  x // Done. All bits have been added.
}

This still won’t optimize down to a popcnt instruction, of course. The search scope for such a simplification is in the regime of superoptimizers. However, the generated code is small and fast, which is why this is the ideal implementation of popcnt for systems without such an instruction.

It’s especially nice because it is implementable for e.g. u64 with only one more reduction step (remember: it’s $O(\log n)$!), and does not at any point require a full u64 addition.

Even though this is “just” using scalars, divide-and-conquer approaches like this are the bread and butter of the SIMD programmer.

Scaling Up: Operations on Real Vectors

Proper SIMD vectors provide more sophisticated semantics than scalars do, particularly because there is more need to provide replacements for things like control flow. Remember, control flow is slow!

What’s actually available is highly dependent on the architecture you’re compiling to (more on this later), but the way vector instruction sets are usually structured is something like this.

We have vector registers that are kind of like really big general-purpose registers. For example, on x86, most “high performance” cores (like my Zen 2) implement AVX2, which provides 256 bit ymm vectors. The registers themselves do not have a “lane count”; that is specified by the instructions. For example, the “vector byte add instruction” interprets the register as being divided into eight-byte lanes and adds them. The corresponding x86 instruction is vpaddb, which interprets a ymm as an i8x32.

The operations you usually get are:

1. Bitwise operations. These don’t need to specify a lane width because it’s always implicitly 1: they’re bitwise.

2. Lane-wise arithmetic. This is addition, subtraction, multiplication, division (both int and float), and shifts¹ (int only). Lane-wise min and max are also common. These require specifying a lane width. Typically the smallest number of lanes is two or four.

3. Lane-wise compare. Given a and b, we can create a new mask vector m such that m[i] = a[i] < b[i] (or any other comparison operation). A mask vector’s lanes contain boolean values with an unusual bit-pattern: all-zeros (for false) or all-ones (for true)².

   • Masks can be used to select between two vectors: for example, given m, x, and y, you can form a fourth vector z such that z[i] = m[i] ? a[i] : b[i].

4. Shuffles (sometimes called swizzles). Given a and x, create a third vector s such that s[i] = a[x[i]]. a is used as a lookup table, and x as a set of indices. Out of bounds produces a special value, usually zero. This emulates parallelized array access without needing to actually touch RAM (RAM is extremely slow).

   • Often there is a “shuffle2” or “riffle” operation that allows taking elements from one of two vectors. Given a, b, and x, we now define s as being s[i] = (a ++ b)[x[i]], where a ++ b is a double-width concatenation. How this is actually implemented depends on architecture, and it’s easy to build out of single shuffles regardless.

(1) and (2) are ordinary number crunching. Nothing deeply special about them.

The comparison and select operations in (3) are intended to help SIMD code stay “branchless”. Branchless code is written such that it performs the same operations regardless of its inputs, and relies on the properties of those operations to produce correct results. For example, this might mean taking advantage of identities like x * 0 = 0 and a ^ b ^ a = b to discard “garbage” results.

The shuffles described in (4) are much more powerful than meets the eye.

For example, “broadcast” (sometimes called “splat”) makes a vector whose lanes are all the same scalar, like Rust’s [42; N] array literal. A broadcast can be expressed as a shuffle: create a vector with the desired value in the first lane, and then shuffle it with an index vector of [0, 0, ...].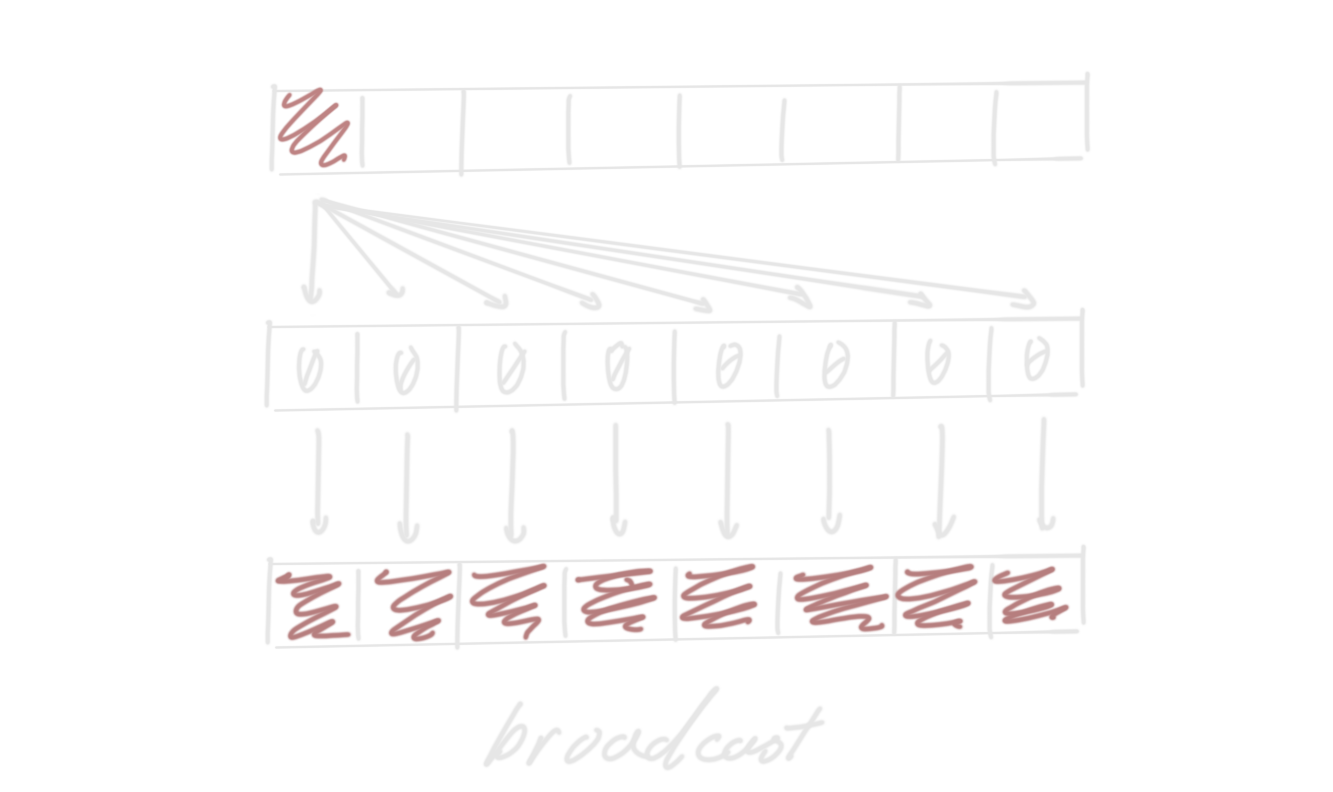

“Interleave” (also called “zip” or “pack”) takes two vectors a and b and creates two new vectors c and d whose lanes are alternating lanes from a and b. If the lane count is n, then c = [a[0], b[0], a[1], b[1], ...] and d = [a[n/2], b[n/2], a[n/2 + 1], b[n/2 + 1], ...]. This can also be implemented as a shuffle2, with shuffle indices of [0, n, 1, n + 1, ...]. “Deinterleave” (or “unzip”, or “unpack”) is the opposite operation: it interprets a pair of vectors as two halves of a larger vector of pairs, and produces two new vectors consisting of the halves of each pair.

Interleave can also be interpreted as taking a [T; N], transmuting it to a [[T; N/2]; 2], performing a matrix transpose to turn it into a [[T; 2]; N/2], and then transmuting that back to [T; N] again. Deinterleave is the same but it transmutes to [[T; 2]; N/2] first.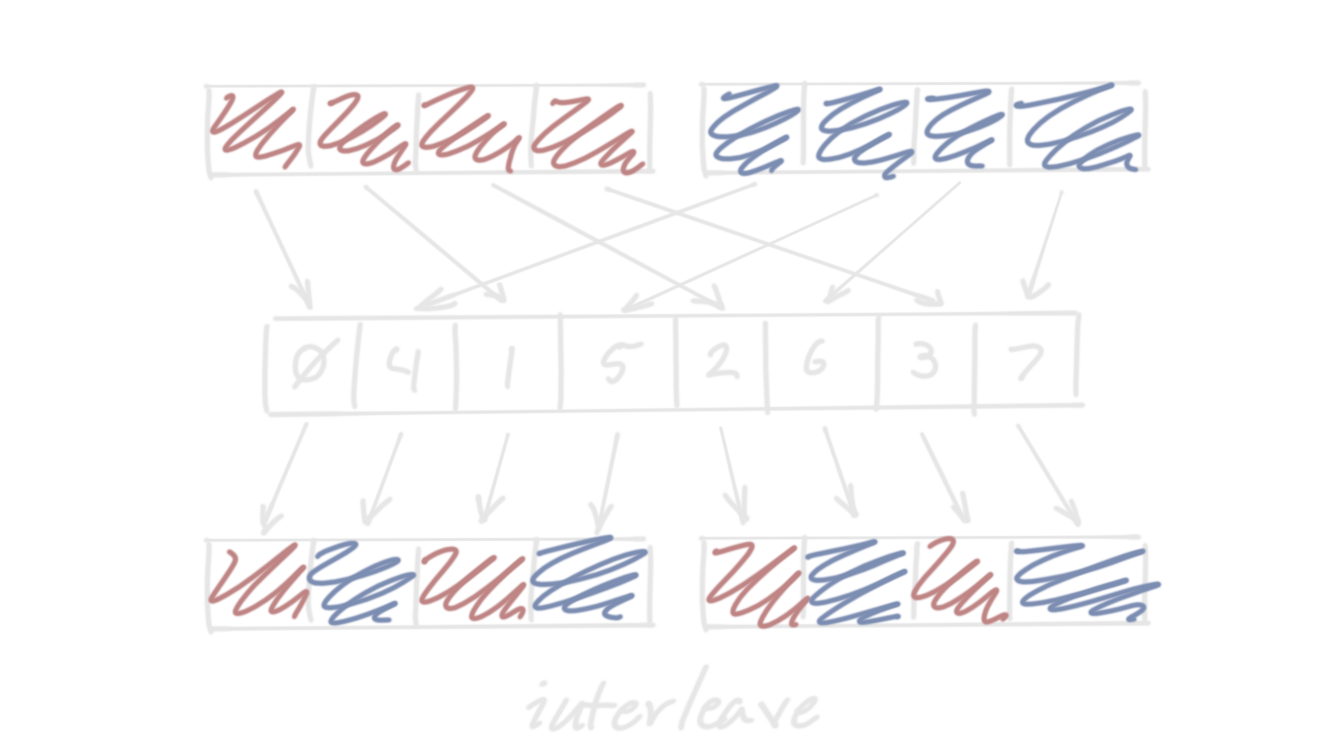

“Rotate” takes a vector a with n lanes and produces a new vector b such that b[i] = a[(i + j) % n], for some chosen integer j. This is yet another shuffle, with indices [j, j + 1, ..., n - 1, 0, 1, ... j - 1].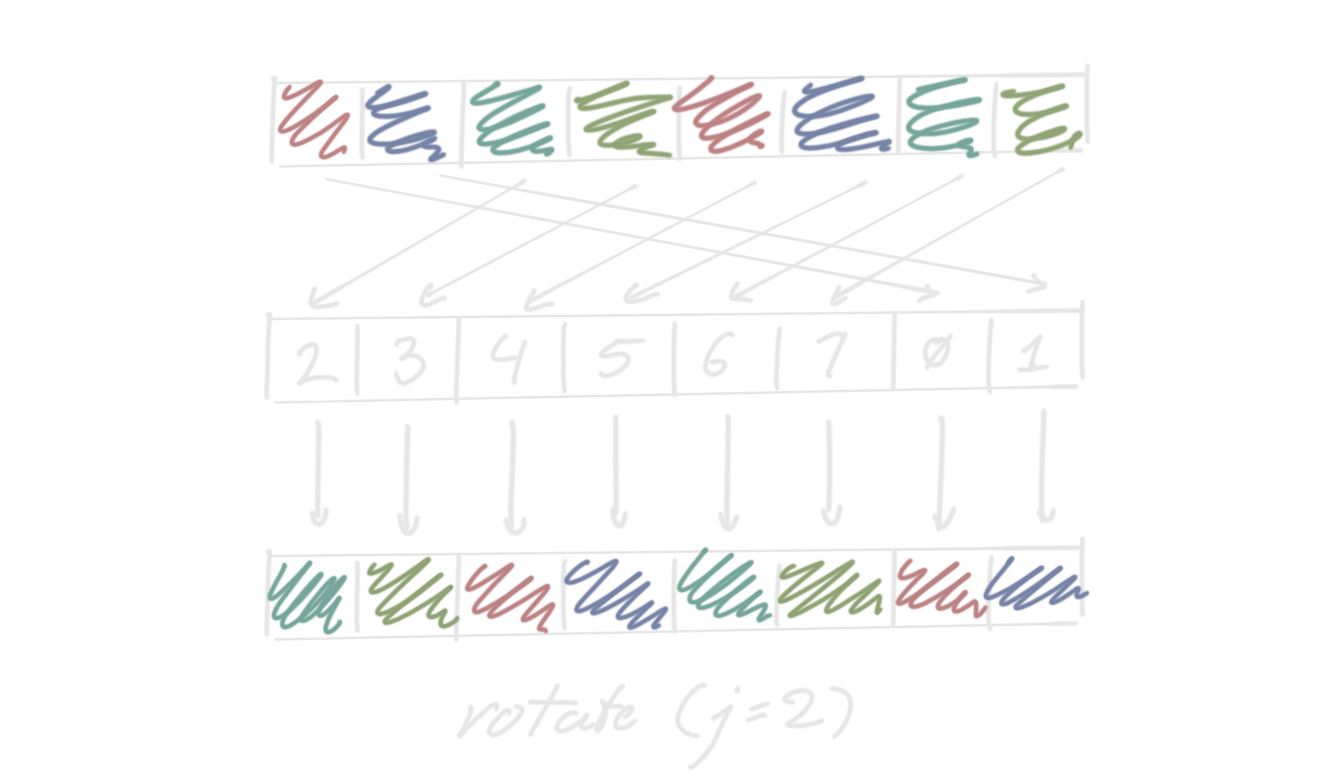

Shuffles are worth trying to wrap your mind around. SIMD programming is all about reinterpreting larger-than-an-integer-sized blocks of data as smaller blocks of varying sizes, and shuffling is important for getting data into the right “place”.

Intrinsics and Instruction Selection

Earlier, I mentioned that what you get varies by architecture. This section is basically a giant footnote.

So, there’s two big factors that go into this.

1. We’ve learned over time which operations tend to be most useful to programmers. x86 might have something that ARM doesn’t because it “seemed like a good idea at the time” but turned out to be kinda niche.
2. Instruction set extensions are often market differentiators, even within the same vendor. Intel has AVX-512, which provides even more sophisticated instructions, but it’s only available on high-end server chips, because it makes manufacturing more expensive.

Toolchains generalize different extensions as “target features”. Features can be detected at runtime through architecture-specific magic. On Linux, the lscpu command will list what features the CPU advertises that it recognizes, which correlate with the names of features that e.g. LLVM understands. What features are enabled for a particular function affects how LLVM compiles it. For example, LLVM will only emit ymm-using code when compiling with +avx2.

So how do you write portable SIMD code? On the surface, the answer is mostly “you don’t”, but it’s more complicated than that, and for that we need to understand how the later parts of a compiler works.

When a user requests an add by writing a + b, how should I decide which instruction to use for it? This seems like a trick question… just an add right? On x86, even this isn’t so easy, since you have a choice between the actual add instruction, or a lea instruction (which, among other things, preserves the rflags register). This question becomes more complicated for more sophisticated operations. This general problem is called instruction selection.

Because which “target features” are enabled affects which instructions are available, they affect instruction selection. When I went over operations “typically available”, this means that compilers will usually be able to select good choices of instructions for them on most architectures.

Compiling with something like -march=native or -Ctarget-cpu=native gets you “the best” code possible for the machine you’re building on, but it might not be portable³ to different processors. Gentoo was quite famous for building packages from source on user machines to take advantage of this (not to mention that they loved using -O3, which mostly exists to slow down build times with little benefit).

There is also runtime feature detection, where a program decides which version of a function to call at runtime by asking the CPU what it supports. Code deployed on heterogenous devices (like cryptography libraries) often make use of this. Doing this correctly is very hard and something I don’t particularly want to dig deeply into here.

The situation is made worse by the fact that in C++, you usually write SIMD code using “intrinsics”, which are special functions with inscrutable names like _mm256_cvtps_epu32 that represent a low-level operation in a specific instruction set (this is a float to int cast from AVX2). Intrinsics are defined by hardware vendors, but don’t necessarily map down to single instructions; the compiler can still optimize these instructions by merging, deduplication, and through instruction selection.

As a result you wind up writing the same code multiple times for different instruction sets, with only minor maintainability benefits over writing assembly.

The alternative is a portable SIMD library, which does some instruction selection behind the scenes at the library level but tries to rely on the compiler for most of the heavy-duty work. For a long time I was skeptical that this approach would actually produce good, competitive code, which brings us to the actual point of this article: using Rust’s portable SIMD library to implement a somewhat fussy algorithm, and measuring performance.

Parsing with SIMD

Let’s design a SIMD implementation for a well-known algorithm. Although it doesn’t look like it at first, the power of shuffles makes it possible to parse text with SIMD. And this parsing can be very, very fast.

In this case, we’re going to implement base64 decoding. To review, base64 is an encoding scheme for arbitrary binary data into ASCII. We interpret a byte slice as a bit vector, and divide it into six-bit chunks called sextets. Then, each sextet from 0 to 63 is mapped to an ASCII character:

1. 0 to 25 go to 'A' to 'Z'.
2. 26 to 51 go to 'a' to 'z'.
3. 52 to 61 go to '0' to '9'.
4. 62 goes to +.
5. 63 goes to /.

There are other variants of base64, but the bulk of the complexity is the same for each variant.

There are a few basic pitfalls to keep in mind.

1. Base64 is a “big endian” format: specifically, the bits in each byte are big endian. Because a sextet can span only parts of a byte, this distinction is important.

2. We need to beware of cases where the input length is not divisible by 4; ostensibly messages should be padded with = to a multiple of 4, but it’s easy to just handle messages that aren’t padded correctly.

The length of a decoded message is given by this function:

fn decoded_len(input: usize) -> usize {
  input / 4 * 3 + match input % 4 {
    1 | 2 => 1,
    3 => 2,
    _ => 0,
  }
}

Given all this, the easiest way to implement base64 is something like this.

fn decode(data: &[u8], out: &mut Vec<u8>) -> Result<(), Error> {
  // Tear off at most two trailing =.
  let data = match data {
    [p @ .., b'=', b'='] | [p @ .., b'='] | p => p,
  };

  // Split the input into chunks of at most 4 bytes.
  for chunk in data.chunks(4) {
    let mut bytes = 0u32;
    for &byte in chunk {
      // Translate each ASCII character into its corresponding
      // sextet, or return an error.
      let sextet = match byte {
        b'A'..=b'Z' => byte - b'A',
        b'a'..=b'z' => byte - b'a' + 26,
        b'0'..=b'9' => byte - b'0' + 52,
        b'+' => 62,
        b'/' => 63,
        _ => return Err(Error(...)),
      };

      // Append the sextet to the temporary buffer.
      bytes <<= 6;
      bytes |= sextet as u32;
    }

    // Shift things so the actual data winds up at the
    // top of `bytes`.
    bytes <<= 32 - 6 * chunk.len();

    // Append the decoded data to `out`, keeping in mind that
    // `bytes` is big-endian encoded.
    let decoded = decoded_len(chunk.len());
    out.extend_from_slice(&bytes.to_be_bytes()[..decoded]);
  }

  Ok(())
}

So, what’s the process of turning this into a SIMD version? We want to follow one directive with inexorable, robotic dedication.

Eliminate all branches.

This is not completely feasible, since the input is of variable length. But we can try. There are several branches in this code:

1. The for chunk in line. This one is is the length check: it checks if there is any data left to process.
2. The for &byte in line. This is the hottest loop: it branches once per input byte.
3. The match byte line is several branches, to determine which of the five “valid” match arms we land in.
4. The return Err line. Returning in a hot loop is extra control flow, which is not ideal.
5. The call to decoded_len contains a match, which generates branches.
6. The call to Vec::extend_from_slice. This contains not just branches, but potential calls into the allocator. Extremely slow.

(5) is the easiest to deal with. The match is mapping the values 0, 1, 2, 3 to 0, 1, 1, 2. Call this function f. Then, the sequence given by x - f(x) is 0, 0, 1, 1. This just happens to equal x / 2 (or x >> 1), so we can write a completely branchless version of decoded_len like so.

pub fn decoded_len(input: usize) -> usize {
  let mod4 = input % 4;
  input / 4 * 3 + (mod4 - mod4 / 2)
}

That’s one branch eliminated⁴. ✅

The others will not prove so easy. Let’s turn our attention to the innermost loop next, branches (2), (3), and (4).

The Hottest Loop

The superpower of SIMD is that because you operate on so much data at a time, you can unroll the loop so hard it becomes branchless.

The insight is this: we want to load at most four bytes, do something to them, and then spit out at most three decoded bytes. While doing this operation, we may encounter a syntax error so we need to report that somehow.

Here’s some facts we can take advantage of.

1. We don’t need to figure out how many bytes are in the “output” of the hot loop: our handy branchless decoded_len() does that for us.
2. Invalid base64 is extremely rare. We want that syntax error to cost as little as possible. If the user still cares about which byte was the problem, they can scan the input for it after the fact.
3. A is zero in base64. If we’re parsing a truncated chunk, padding it with A won’t change the value⁵.

This suggests an interface for the body of the “hottest loop”. We can factor it out as a separate function, and simplify since we can assume our input is always four bytes now.

fn decode_hot(ascii: [u8; 4]) -> ([u8; 3], bool) {
  let mut bytes = 0u32;
  let mut ok = true;
  for byte in ascii {
    let sextet = match byte {
      b'A'..=b'Z' => byte - b'A',
      b'a'..=b'z' => byte - b'a' + 26,
      b'0'..=b'9' => byte - b'0' + 52,
      b'+' => 62,
      b'/' => 63,
      _ => !0,
    };

    bytes <<= 6;
    bytes |= sextet as u32;
    ok &= byte == !0;
  }

  // This is the `to_be_bytes()` call.
  let [b1, b2, b3, _] = bytes.to_le_bytes();
  ([b3, b2, b1], ok)
}

// In decode()...
for chunk in data.chunks(4) {
  let mut ascii = [b'A'; 4];
  ascii[..chunk.len()].copy_from_slice(chunk);

  let (bytes, ok) = decode_hot(ascii);
  if !ok {
    return Err(Error)
  }

  let len = decoded_len(chunk.len());
  out.extend_from_slice(&bytes[..decoded]);
}

You’re probably thinking: why not return Option<[u8; 3]>? Returning an enum will make it messier to eliminate the if !ok branch later on (which we will!). We want to write branchless code, so let’s focus on finding a way of producing that three-byte output without needing to do early returns.

Now’s when we want to start talking about vectors rather than arrays, so let’s try to rewrite our function as such.

fn decode_hot(ascii: Simd<u8, 4>) -> (Simd<u8, 4>, bool) {
  unimplemented!()
}

Note that the output is now four bytes, not three. SIMD lane counts need to be powers of two, and that last element will never get looked at, so we don’t need to worry about what winds up there.

The callsite also needs to be tweaked, but only slightly, because Simd<u8, 4> is From<[u8; 4]>.

ASCII to Sextet

Let’s look at the first part of the for byte in ascii loop. We need to map each lane of the Simd<u8, 4> to the corresponding sextet, and somehow signal which ones are invalid. First, notice something special about the match: almost every arm can be written as byte - C for some constant C. The non-range case looks a little silly, but humor me:

let sextet = match byte {
  b'A'..=b'Z' => byte - b'A',
  b'a'..=b'z' => byte - b'a' + 26,
  b'0'..=b'9' => byte - b'0' + 52,
  b'+'        => byte - b'+' + 62,
  b'/'        => byte - b'/' + 63,
  _ => !0,
};

So, it should be sufficient to build a vector offsets that contains the appropriate constant C for each lane, and then let sextets = ascii - offsets;

How can we build offsets? Using compare-and-select.

// A lane-wise version of `x >= start && x <= end`.
fn in_range(bytes: Simd<u8, 4>, start: u8, end: u8) -> Mask<i8, 4> {
  bytes.simd_ge(Simd::splat(start)) & bytes.simd_le(Simd::splat(end))
}

// Create masks for each of the five ranges.
// Note that these are disjoint: for any two masks, m1 & m2 == 0.
let uppers = in_range(ascii, b'A', b'Z');
let lowers = in_range(ascii, b'a', b'z');
let digits = in_range(ascii, b'0', b'9');
let pluses = ascii.simd_eq([b'+'; N].into());
let solidi = ascii.simd_eq([b'/'; N].into());

// If any byte was invalid, none of the masks will select for it,
// so that lane will be 0 in the or of all the masks. This is our
// validation check.
let ok = (uppers | lowers | digits | pluses | solidi).all();

// Given a mask, create a new vector by splatting `value`
// over the set lanes.
fn masked_splat(mask: Mask<i8, N>, value: i8) -> Simd<i8, 4> {
  mask.select(Simd::splat(val), Simd::splat(0))
}

// Fill the the lanes of the offset vector by filling the
// set lanes with the corresponding offset. This is like
// a "vectorized" version of the `match`.
let offsets = masked_splat(uppers,  65)
            | masked_splat(lowers,  71)
            | masked_splat(digits,  -4)
            | masked_splat(pluses, -19)
            | masked_splat(solidi, -16);

// Finally, Build the sextets vector.
let sextets = ascii.cast::<i8>() - offsets;

This solution is quite elegant, and will produce very competitive code, but it’s not actually ideal. We need to do a lot of comparisons here: eight in total. We also keep lots of values alive at the same time, which might lead to unwanted register pressure.

SIMD Hash Table

Let’s look at the byte representations of the ranges. A-Z, a-z, and 0-9 are, as byte ranges, 0x41..0x5b, 0x61..0x7b, and 0x30..0x3a. Notice they all have different high nybbles! What’s more, + and / are 0x2b and 0x2f, so the function byte >> 4 is almost enough to distinguish all the ranges. If we subtract one if byte == b'/', we have a perfect hash for the ranges.

In other words, the value (byte >> 4) - (byte == '/') maps the ranges as follows:

• A-Z goes to 4 or 5.
• a-z goes to 6 or 7.
• 0-9 goes to 3.
• + goes to 2.
• / goes to 1.

This is small enough that we could cram a lookup table of values for building the offsets vector into another SIMD vector, and use a shuffle operation to do the lookup.

This is not my original idea; I came across a GitHub issue where an anonymous user points out this perfect hash.

Our new ascii-to-sextet code looks like this:

// Compute the perfect hash for each lane.
let hashes = (ascii >> Simd::splat(4))
  + Simd::simd_eq(ascii, Simd::splat(b'/'))
    .to_int()  // to_int() is equivalent to masked_splat(-1, 0).
    .cast::<u8>();

// Look up offsets based on each hash and subtract them from `ascii`.
let sextets = ascii
    // This lookup table corresponds to the offsets we used to build the
    // `offsets` vector in the previous implementation, placed in the
    // indices that the perfect hash produces.
  - Simd::<i8, 8>::from([0, 16, 19, 4, -65, -65, -71, -71])
    .cast::<u8>()
    .swizzle_dyn(hashes);

There is a small wrinkle here: Simd::swizzle_dyn() requires that the index array be the same length as the lookup table. This is annoying because right now ascii is a Simd<u8, 4>, but that will not be the case later on, so I will simply sweep this under the rug.

Note that we no longer get validation as a side-effect of computing the sextets vector. The same GitHub issue also provides an exact bloom-filter for checking that a particular byte is valid; you can see my implementation here. I’m not sure how the OP constructed the bloom filter, but the search space is small enough that you could have written a little script to brute force it.

Riffling the Sextets

Now comes a much tricker operation: we need to somehow pack all four sextets into three bytes. One way to try to wrap our head around what the packing code in decode_hot() is doing is to pass in the all-ones sextet in one of the four bytes, and see where those ones end up in the return value.

This is not unlike how they use radioactive dyes in biology to track the moment of molecules or cells through an organism.

fn bits(value: u32) -> String {
  let [b1, b2, b3, b4] = value.reverse_bits().to_le_bytes();
  format!("{b1:08b} {b2:08b} {b3:08b} {b4:08b}")
}

fn decode_pack(input: [u8; 4]) {
  let mut output = 0u32;
  for byte in input {
    output <<= 6;
    output |= byte as u32;
  }
  output <<= 8;

  println!("{}\n{}\n", bits(u32::from_be_bytes(input)), bits(output));
}

decode_pack([0b111111, 0, 0, 0]);
decode_pack([0, 0b111111, 0, 0]);
decode_pack([0, 0, 0b111111, 0]);
decode_pack([0, 0, 0, 0b111111]);

// Output:
// 11111100 00000000 00000000 00000000
// 00111111 00000000 00000000 00000000
//
// 00000000 11111100 00000000 00000000
// 11000000 00001111 00000000 00000000
//
// 00000000 00000000 11111100 00000000
// 00000000 11110000 00000011 00000000
//
// 00000000 00000000 00000000 11111100
// 00000000 00000000 11111100 00000000

Bingo. Playing around with the inputs lets us verify which pieces of the bytes wind up where. For example, by passing 0b110000 as input[1], we see that the two high bits of input[1] correspond to the low bits of output[0]. I’ve written the code so that the bits in each byte are printed in little-endian order, so bits on the left are the low bits.

Putting this all together, we can draw a schematic of what this operation does to a general Simd<u8, 4>.

Now, there’s no single instruction that will do this for us. Shuffles can be used to move bytes around, but we’re dealing with pieces of bytes here. We also can’t really do a shift, since we need bits that are overshifted to move into adjacent lanes.

The trick is to just make the lanes bigger.

Among the operations available for SIMD vectors are lane-wise casts, which allow us to zero-extend, sign-extend, or truncate each lane. So what we can do is cast sextets to a vector of u16, do the shift there and then… somehow put the parts back together?

Let’s see how far shifting gets us. How much do we need to shift things by? First, notice that the order of the bits within each chunk that doesn’t cross a byte boundary doesn’t change. For example, the four low bits of input[1] are in the same order when they become the high bits of output[1], and the two high bits of input[1] are also in the same order when they become the low bits of output[0].

This means we can determine how far to shift by comparing the bit position of the lowest bit of a byte of input with the bit position of the corresponding bit in output.

input[0]’s low bit is the third bit of output[0], so we need to shift input[0] by 2. input[1]’s lowest bit is the fifth bit of output[1], so we need to shift by 4. Analogously, the shifts for input[2] and input[3] turn out to be 6 and 0. In code:

let sextets = ...;
let shifted = sextets.cast::<u16>() << Simd::from([2, 4, 6, 0]);

So now we have a Simd<u16, 4> that contains the individual chunks that we need to move around, in the high and low bytes of each u16, which we can think of as being analogous to a [[u8; 2]; 4]. For example, shifted[0][0] contains sextet[0], but shifted. This corresponds to the red segment in the first schematic. The smaller blue segment is given by shifted[1][1], i.e., the high byte of the second u16. It’s already in the right place within that byte, so we want output[0] = shifted[0][0] | shifted[1][1].

This suggests a more general strategy: we want to take two vectors, the low bytes and the high bytes of each u16 in shifted, respectively, and somehow shuffle them so that when or’ed together, they give the desired output.

Look at the schematic again: if we had a vector consisting of [..aaaaaa, ....bbbb, ......cc], we could or it with a vector like [bb......, cccc...., dddddd..] to get the desired result.

One problem: dddddd.. is shifted[3][0], i.e., it’s a low byte. If we change the vector we shift by to [2, 4, 6, 8], though, it winds up in shifted[3][1], since it’s been shifted up by 8 bits: a full byte.

// Split shifted into low byte and high byte vectors.
// Same way you'd split a single u16 into bytes, but lane-wise.
let lo = shifted.cast::<u8>();
let hi = (shifted >> Simd::from([8; 4])).cast::<u8>();

// Align the lanes: we want to get shifted[0][0] | shifted[1][1],
// shifted[1][0] | shifted[2][1], etc.
let output = lo | hi.rotate_lanes_left::<1>();

Et voila, here is our new, totally branchless implementation of decode_hot().

fn decode_hot(ascii: Simd<u8, 4>) -> (Simd<u8, 4>, bool) {
  let hashes = (ascii >> Simd::splat(4))
    + Simd::simd_eq(ascii, Simd::splat(b'/'))
      .to_int()
      .cast::<u8>();

  let sextets = ascii
    - Simd::<i8, 8>::from([0, 16, 19, 4, -65, -65, -71, -71])
      .cast::<u8>()
      .swizzle_dyn(hashes);  // Note quite right yet, see next section.

  let ok = /* bloom filter shenanigans */;

  let shifted = sextets.cast::<u16>() << Simd::from([2, 4, 6, 8]);
  let lo = shifted.cast::<u8>();
  let hi = (shifted >> Simd::splat(8)).cast::<u8>();
  let output = lo | hi.rotate_lanes_left::<1>();

  (output, ok)
}

The compactness of this solution should not be understated. The simplicity of this solution is a large part of what makes it so efficient, because it aggressively leverages the primitives the hardware offers us.

Scaling Up

Ok, so now we have to contend with a new aspect of our implementation that’s crap: a Simd<u8, 4> is tiny. That’s not even 128 bits, which are the smallest vector registers on x86. What we need to do is make decode_hot() generic on the lane count. This will allow us to tune the number of lanes to batch together depending on benchmarks later on.

fn decode_hot<const N: usize>(ascii: Simd<u8, N>) -> (Simd<u8, N>, bool)
where
  // This makes sure N is a small power of 2.
  LaneCount<N>: SupportedLaneCount,
{
  let hashes = (ascii >> Simd::splat(4))
    + Simd::simd_eq(ascii, Simd::splat(b'/'))
      .to_int()
      .cast::<u8>();

  let sextets = ascii
    - tiled(&[0, 16, 19, 4, -65, -65, -71, -71])
      .cast::<u8>()
      .swizzle_dyn(hashes);  // Works fine now, as long as N >= 8.

  let ok = /* bloom filter shenanigans */;

  let shifted = sextets.cast::<u16>() << tiled(&[2, 4, 6, 8]);
  let lo = shifted.cast::<u8>();
  let hi = (shifted >> Simd::splat(8)).cast::<u8>();
  let output = lo | hi.rotate_lanes_left::<1>();

  (output, ok)
}

/// Generates a new vector made up of repeated "tiles" of identical
/// data.
const fn tiled<T, const N: usize>(tile: &[T]) -> Simd<T, N>
where
  T: SimdElement,
  LaneCount<N>: SupportedLaneCount,
{
  let mut out = [tile[0]; N];
  let mut i = 0;
  while i < N {
    out[i] = tile[i % tile.len()];
    i += 1;
  }
  Simd::from_array(out)
}

We have to change virtually nothing, which is pretty awesome! But unfortunately, this code is subtly incorrect. Remember how in the N = 4 case, the result of output had a garbage value that we ignore in its highest lane? Well, now that garbage data is interleaved into output: every fourth lane contains garbage.

We can use a shuffle to delete these lanes, thankfully. Specifically, we want shuffled[i] = output[i + i / 3], which skips every forth index. So, shuffled[3] = output[4], skipping over the garbage value in output[3]. If i + i / 3 overflows N, that’s ok, because that’s the high quarter of the final output vector, which is ignored anyways. In code:

fn decode_hot<const N: usize>(ascii: Simd<u8, N>) -> (Simd<u8, N>, bool)
where
  // This makes sure N is a small power of 2.
  LaneCount<N>: SupportedLaneCount,
{
  /* snip */

  let decoded_chunks = lo | hi.rotate_lanes_left::<1>();
  let output = swizzle!(N; decoded_chunks, array!(N; |i| i + i / 3));

  (output, ok)
}

swizzle!() is a helper macro⁶ for generating generic implementations of std::simd::Swizzle, and array!() is something I wrote for generating generic-length array constants; the closure is called once for each i in 0..N.

So now we can decode 32 base64 bytes in parallel by calling decode_hot::<32>(). We’ll try to keep things generic from here, so we can tune the lane parameter based on benchmarks.

The Outer Loop

Let’s look at decode() again. Let’s start by making it generic on the internal lane count, too.

fn decode<const N: usize>(data: &[u8], out: &mut Vec<u8>) -> Result<(), Error>
where
  LaneCount<N>: SupportedLaneCount,
{
  let data = match data {
    [p @ .., b'=', b'='] | [p @ .., b'='] | p => p,
  };

  for chunk in data.chunks(N) { // N-sized chunks now.
    let mut ascii = [b'A'; N];
    ascii[..chunk.len()].copy_from_slice(chunk);

    let (dec, ok) = decode_hot::<N>(ascii.into());
    if (!ok) {
      return Err(Error);
    }

    let decoded = decoded_len(chunk.len());
    out.extend_from_slice(&dec[..decoded]);
  }

  Ok(())
}

What branches are left? There’s still the branch from for chunks in .... It’s not ideal because it can’t do an exact pointer comparison, and needs to do a >= comparison on a length instead.

We call [T]::copy_from_slice, which is super slow because it needs to make a variable-length memcpy call, which can’t be inlined. Function calls are branches! The bounds checks are also a problem.

We branch on ok every loop iteration, still. Not returning early in decode_hot doesn’t win us anything (yet).

We potentially call the allocator in extend_from_slice, and perform another non-inline-able memcpy call.

Preallocating with Slop

The last of these is the easiest to address: we can reserve space in out, since we know exactly how much data we need to write thanks to decoded_len. Better yet, we can reserve some “slop”: i.e., scratch space past where the end of the message would be, so we can perform full SIMD stores, instead of the variable-length memcpy.

This way, in each iteration, we write the full SIMD vector, including any garbage bytes in the upper quarter. Then, the next write is offset 3/4 * N bytes over, so it overwrites the garbage bytes with decoded message bytes. The garbage bytes from the final right get “deleted” by not being included in the final Vec::set_len() that “commits” the memory we wrote to.

fn decode<const N: usize>(data: &[u8], out: &mut Vec<u8>) -> Result<(), Error>
where LaneCount<N>: SupportedLaneCount,
{
  let data = match data {
    [p @ .., b'=', b'='] | [p @ .., b'='] | p => p,
  };

  let final_len = decoded_len(data);
  out.reserve(final_len + N / 4);  // Reserve with slop.

  // Get a raw pointer to where we should start writing.
  let mut ptr = out.as_mut_ptr_range().end();
  let start = ptr;

  for chunk in data.chunks(N) { // N-sized chunks now.
    /* snip */

    let decoded = decoded_len(chunk.len());
    unsafe {
      // Do a raw write and advance the pointer.
      ptr.cast::<Simd<u8, N>>().write_unaligned(dec);
      ptr = ptr.add(decoded);
    }
  }

  unsafe {
    // Update the vector's final length.
    // This is the final "commit".
    let len = ptr.offset_from(start);
    out.set_len(len as usize);
  }

  Ok(())
}

This is safe, because we’ve pre-allocated exactly the amount of memory we need, and where ptr lands is equal to the amount of memory actually decoded. We could also compute the final length of out ahead of time.

Note that if we early return due to if !ok, out remains unmodified, because even though we did write to its buffer, we never execute the “commit” part, so the code remains correct.

Delaying Failure

Next up, we can eliminate the if !ok branches by waiting to return an error until as late as possible: just before the set_len call.

Remember our observation from before: most base64 encoded blobs are valid, so this unhappy path should be very rare. Also, syntax errors cannot cause code that follows to misbehave arbitrarily, so letting it go wild doesn’t hurt anything.

fn decode<const N: usize>(data: &[u8], out: &mut Vec<u8>) -> Result<(), Error>
where LaneCount<N>: SupportedLaneCount,
{
  /* snip */
  let mut error = false;
  for chunk in data.chunks(N) {
    let mut ascii = [b'A'; N];
    ascii[..chunk.len()].copy_from_slice(chunk);

    let (dec, ok) = decode_hot::<N>(ascii.into());
    error |= !ok;

    /* snip */
  }

  if error {
    return Err(Error);
  }

  unsafe {
    let len = ptr.offset_from(start);
    out.set_len(len as usize);
  }

  Ok(())
}

The branch is still “there”, sure, but it’s out of the hot loop.

Because we never hit the set_len call and commit whatever garbage we wrote, said garbage essentially disappears when we return early, to be overwritten by future calls to Vec::push().

Unroll It Harder

Ok, let’s look at the memcpy from copy_from_slice at the start of the hot loop. The loop has already been partly unrolled: it does N iterations with SIMD each step, doing something funny on the last step to make up for the missing data (padding with A).

We can take this a step further by doing an “unroll and jam” optimization. This type of unrolling splits the loop into two parts: a hot vectorized loop and a cold remainder part. The hot loop always handles length N input, and the remainder runs at most once and handles i < N input.

Rust provides an iterator adapter for hand-rolled (lol) unroll-and-jam: Iterator::chunks_exact().

fn decode<const N: usize>(data: &[u8], out: &mut Vec<u8>) -> Result<(), Error>
where LaneCount<N>: SupportedLaneCount,
{
  /* snip */
  let mut error = false;
  let mut chunks = data.chunks_exact(N);
  for chunk in &mut chunks {
    // Simd::from_slice() can do a load in one instruction.
    // The bounds check is easy for the compiler to elide.
    let (dec, ok) = decode_hot::<N>(Simd::from_slice(chunk));
    error |= !ok;
    /* snip */
  }

  let rest = chunks.remainder();
  if !rest.empty() {
    let mut ascii = [b'A'; N];
    ascii[..chunk.len()].copy_from_slice(chunk);

    let (dec, ok) = decode_hot::<N>(ascii.into());
    /* snip */
  }

  /* snip */
}

Splitting into two parts lets us call Simd::from_slice(), which performs a single, vector-sized load.

So, How Fast Is It?

At this point, it looks like we’ve addressed every branch that we can, so some benchmarks are in order. I wrote a benchmark that decodes messages of every length from 0 to something like 200 or 500 bytes, and compared it against the baseline base64 implementation on crates.io.

I compiled with -Zbuild-std and -Ctarget-cpu=native to try to get the best results. Based on some tuning, N = 32 was the best length, since it used one YMM register for each iteration of the hot loop.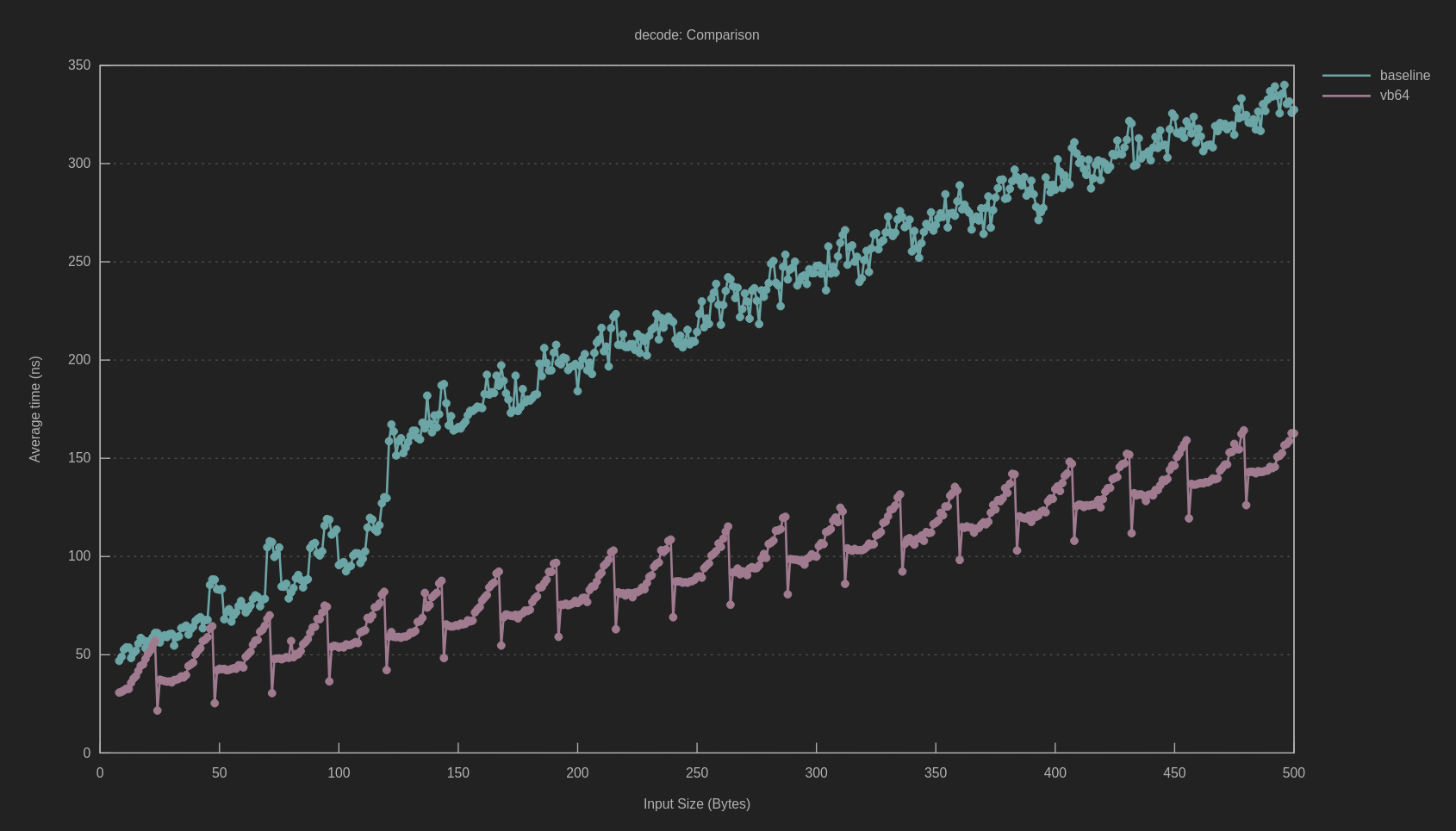

So, we have the baseline beat. But what’s up with that crazy heartbeat waveform? You can tell it has something to do with the “remainder” part of the loop, since it correlates strongly with data.len() % 32.

I stared at the assembly for a while. I don’t remember what was there, but I think that copy_from_slice had been inlined and unrolled into a loop that loaded each byte at a time. The moral equivalent of this:

let mut ascii = [b'A'; N];
for (a, b) in Iterator::zip(&mut ascii, chunk) {
  *a = *b;
}

I decided to try Simd::gather_or(), which is kind of like a “vectorized load”. It wound up producing worse assembly, so I gave up on using a gather and instead wrote a carefully optimized loading function by hand.

Unroll and Jam, Revisited

The idea here is to perform the largest scalar loads Rust offers where possible. The strategy is again unroll and jam: perform u128 loads in a loop and deal with the remainder separately.

The hot part looks like this:

let mut buf = [b'A'; N];

// Load a bunch of big 16-byte chunks. LLVM will lower these to XMM loads.
let ascii_ptr = buf.as_mut_ptr();
let mut write_at = ascii_ptr;
if slice.len() >= 16 {
  for i in 0..slice.len() / 16 {
    unsafe {
      write_at = write_at.add(i * 16);

      let word = slice.as_ptr().cast::<u128>().add(i).read_unaligned();
      write_at.cast::<u128>().write_unaligned(word);
    }
  }
}

The cold part seems hard to optimize at first. What’s the least number of unaligned loads you need to do to load 15 bytes from memory? It’s two! You can load a u64 from p, and then another one from p + 7; these loads (call them a and b) overlap by one byte, but we can or them together to merge that byte, so our loaded value is a as u128 | (b as u128 << 56).

A similar trick works if the data to load is between a u32 and a u64. Finally, to load 1, 2, or 3 bytes, we can load p, p + len/2 and p + len-1; depending on whether len is 1, 2, or 3, this will potentially load the same byte multiple times; however, this reduces the number of branches necessary, since we don’t need to distinguish the 1, 2, or 3 lines.

This is the kind of code that’s probably easier to read than to explain.

unsafe {
  let ptr = slice.as_ptr().offset(write_at.offset_from(ascii_ptr));
  let len = slice.len() % 16;

  if len >= 8 {
    // Load two overlapping u64s.
    let lo = ptr.cast::<u64>().read_unaligned() as u128;
    let hi = ptr.add(len - 8).cast::<u64>().read_unaligned() as u128;
    let data = lo | (hi << ((len - 8) * 8));

    let z = u128::from_ne_bytes([b'A'; 16]) << (len * 8);
    write_at.cast::<u128>().write_unaligned(data | z);
  } else if len >= 4 {
    // Load two overlapping u32s.
    let lo = ptr.cast::<u32>().read_unaligned() as u64;
    let hi = ptr.add(len - 4).cast::<u32>().read_unaligned() as u64;
    let data = lo | (hi << ((len - 4) * 8));

    let z = u64::from_ne_bytes([b'A'; 8]) << (len * 8);
    write_at.cast::<u64>().write_unaligned(data | z);
  } else {
    // Load 3 overlapping u8s.

    // For len       1       2       3     ...
    // ... this is  ptr[0]  ptr[0]  ptr[0]
    let lo = ptr.read() as u32;
    // ... this is  ptr[0]  ptr[1]  ptr[1]
    let mid = ptr.add(len / 2).read() as u32;
    // ... this is  ptr[0]  ptr[1]  ptr[2]
    let hi = ptr.add(len - 1).read() as u32;

    let data = lo | (mid << ((len / 2) * 8)) | hi << ((len - 1) * 8);

    let z = u32::from_ne_bytes([b'A'; 4]) << (len * 8);
    write_at.cast::<u32>().write_unaligned(data | z);
  }
}

I learned this type of loading code while contributing to Abseil: it’s very useful for loading variable-length data for data-hungry algorithms, like a codec or a hash function.

Here’s the same benchmark again, but with our new loading code.

The results are really, really good. The variance is super tight, and our performance is 2x that of the baseline pretty much everywhere. Success.

Encoding? Web-Safe?

Writing an encoding function is simple enough: first, implement an encode_hot() function that reverses the operations from decode_hot(). The perfect hash from before won’t work, so you’ll need to invent a new one.

Also, the loading/storing code around the encoder is slightly different, too. vb64 implements a very efficient encoding routine too, so I suggest taking a look at the source code if you’re interested.

There is a base64 variant called web-safe base64, that replaces the + and / characters with - and _. Building a perfect hash for these is trickier: you would probably have to do something like (byte >> 4) - (byte == '_' ? '_' : 0). I don’t support web-safe base64 yet, but only because I haven’t gotten around to it.

Conclusion

My library doesn’t really solve an important problem; base64 decoding isn’t a bottleneck… anywhere that I know of, really. But writing SIMD code is really fun! Writing branchless code is often overkill but can give you a good appreciation for what your compilers can and can’t do for you.

This project was also an excuse to try std::simd. I think it’s great overall, and generates excellent code. There’s some rough edges I’d like to see fixed to make SIMD code even simpler, but overall I’m very happy with the work that’s been done there.

This is probably one of the most complicated posts I’ve written in a long time. SIMD (and performance in general) is a complex topic that requires a breadth of knowledge of tricks and hardware, a lot of which isn’t written down. More of it is written down now, though.